Fechando nossa série sobre cartas de controles, vamos falar hoje sobre cartas de controle para dados atributivos aplicadas em contagem de feitos.
Pausa Rápida!
No post da semana passada abordamos cartas atributivas aplicadas em percentual e ou proporção de defeitos (Outras Cartas de Controle (Xbarra S; P e NP). Basicamente respondemos se o percetual de falha e/ou proporção de falhas ao longo dos dados coletados era algo “esperado” ou não.
Assim como as cartas N e NP, as cartas U e C são aplicadas em função do subgrupo ser constante ou não.
A carta U é utilizada quando os subgrupos não possuem tamanhos constantes e quando queremos contar o número de defeitos por grupo amostrado.
Supondo nosso exemplo anterior sobre potes! Imagine agora que lotes serão analisados em função de falhas como arranhão, bolhas e falhas de vedação. Abaixo segue um exemplo do que encontramos:

Isso está normal? Algum dia algo saiu fora do esperado?
Vamos analisar!
Primeiro calculamos a taxa de defeitos por amostra dividindo defeito por tamanho de amostra ( por exemplo: 8/125)

Agora calculamos a média de defeitos: 29/609 = 0,0476.
E por fim os limites de cada subgrupo são calculados por:
Limite superior = Ubarra + 3xsqrt(Ubarra/numero de defeitos)
para o primeiro ponto teremos = 0,0476 + 3*sqrt(0,0476/125) = 0,1062
Da mesma forma, calculamos os limites inferiores utilizando:
Limite inferior = Ubarra – 3xsqrt(Ubarra/numero de defeitos)
para o primeiro ponto teremos = 0,0476 – 3*sqrt(0,0476/125) = -0,0109 (faz sentido ter menos de 0 defeitos?- não, entçao sempre que o valor for menor que 0 assuma 0.
Assim temos nossa tabela para a carta:
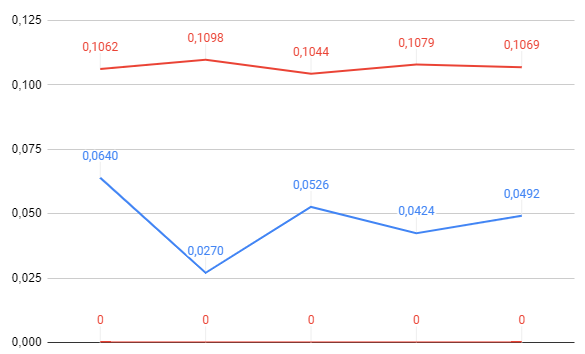
Logo concluímos que o número de falhas que estamos observando em cada amostra é esperado.
Se o tamanho da amostra fosse constante, teríamos que usar a carta C!
Vamos ao exemplo?

Para a carta C utilizamos os próprios números de falhas como entradas.
Em seguida calculamos o valor médio de defeitos somando os números de defeitos e dividindo-o pelo número de amostras:
Cbarra = (8+3+7+5+6)/5 = 5,80
E por fim seus limites superiores e inferiores considerando Cbarra +- 3(sqrt(Cbarra))
Limite Superior = 5,80 + 3*(sqrt(5,8)) = 13,02
Limite Inferior = 5,80 – 3*(sqrt(5,8)) = -1,42 = 0 (mesmo racional da carta U)
A carta desse conjunto de dados é mostrada abaixo:
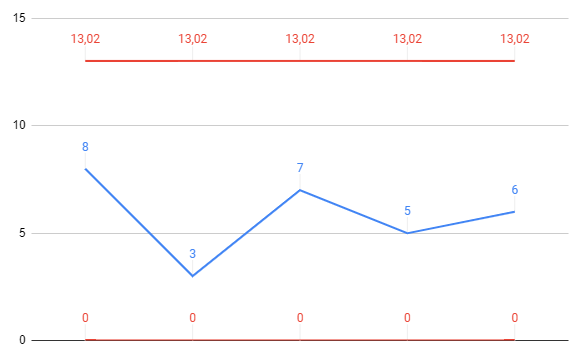
E assim como a anterior podemos ter a seguinte conclusão: o número médio de defeitos é de 13,02 por amostra e o processo se encontra sob controle.
Como mencionado no início, este post termina o bloco sobre Cartas de Controle. Este bloco é extremamente valioso e útil no dia a dia de qualquer engenheiro, farmacêutico, dono de bar, enfim todas as pessoas que trabalham em algo e tenham a necessidade de entender a variação.
Espero que vocês façam bom proveito do material compartilhado e caso tenham dúvidas, não exitem em nos procurar!
Até a próxima