Nos últimos dois posts falamos sobre as cartas XbarraR e IMR, que são as cartas de controle mais conhecidas e utilizadas, no entanto existem algumas outras, menos famosas, porém úteis que vamos discutir hoje.
Xbarra S
Esta carta é similar a carta Xbarra R, mas em vez de considerar o “range” para a análise, utiliza-se a dispersão.
O uso do desvio padrão, dispersão, é indicado quando temos subgrupos grandes, geralmente maiores ou iguais a 10. As demais recomendações de uso são semelhantes a carta XbarraR.
Os limites de controles desta carta são calculados ligeiramente diferente da carta R:
Limite de controle inferior carta S = B3 x Sbarra
Limite de controle superior carta S = B4 x Sbarra
onde Sbarra é a média dos desvios padrão de cada subgrupo.
Limite de controle inferior carta Xbarra = Xbarra barra (média das médias de cada subgrupo) – A3 x Sbarra
Limite de controle superior da carta Xbarra = Xbarra barra + A3 x Sbarra
Cartas de Atributos
As cartas de atributos são utilizadas quando temos os elementos em estudo classificados em categorias, por exemplo (aprovado/reprovado); ou seja complementam as cartas de controle para dados contínuos vistas até aqui.
Existem cartas que expressam o percentual ou proporção de itens reprovados, por exemplo, são estas cartas P e NP. E existem cartas utilizadas para contar os defeitos da reprova, por exemplo, são as cartas U e C.
As cartas NP e C requerem que o tamanho das amostras entre os subgrupos seja constante; já as cartas P e U permitem tamanhos de amostras distintos.
Vamos a alguns exemplos para facilitar o entendimento da aplicação dessas cartas?
Image que você produza potinhos herméticos e ao longo de uma semana de produção você obteve:

Primeiramente, como o tamanho das amostras não é constante, devemos usar a carta P
Como é um carta de proporções, devemos calcular a proporção de cada subgrupo amostrado (exemplo 12/115 = 0,104)
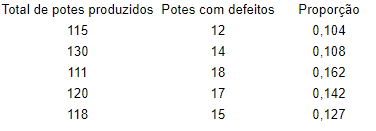
Depois calculamos a proporção média:
Pbarra = (12+14+18+17+15) / (115+130+111+120+118) =0,1279461279
Depois deve-se calcular os limites de cada subgrupo, por exemplo para o último subgrupo temos:
Limite inferior de controle = Pbarra – 3xraiz[Pbarra(1-Pbarra)/n] = 0,128 – 3*sqrt[0,128*(1-0,128)/118] =0,0357
Limite superior de controle = Pbarra + 3xraiz[Pbarra(1-Pbarra)/n] = 0,128 + 3*sqrt[0,128*(1-0,128)/118] =0,220
E agora plotamos a proporção e os limites:
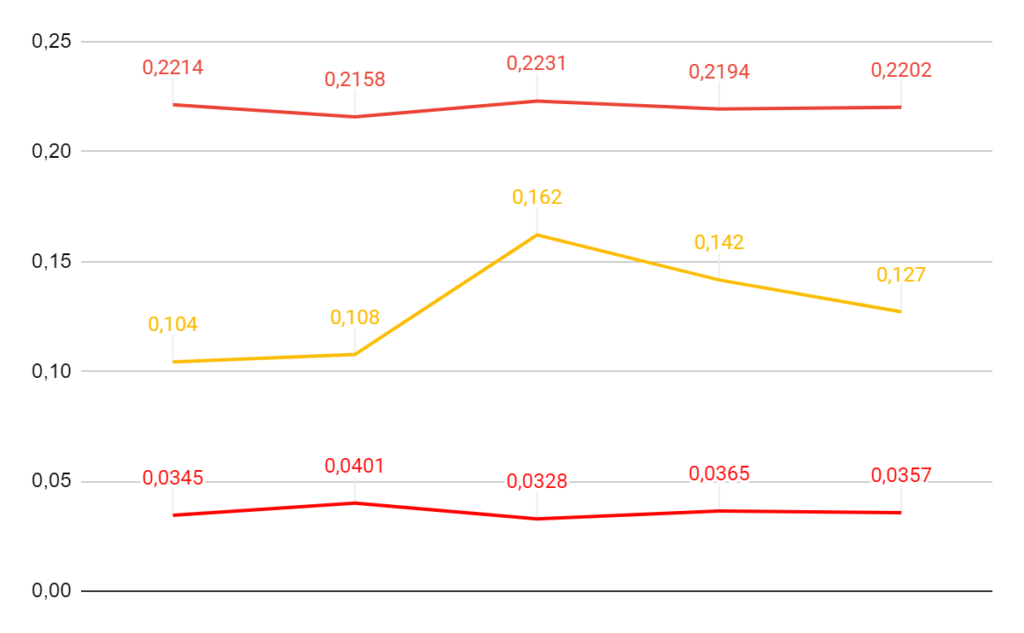
A interpretação é :
Em média temos 12,7% de peças reprovadas. Nenhuma das proporções dos subgrupos está fora dos limites de controle.
Além disso, os pontos dentro dos limites apresentam um padrão aleatório. Esta carta P não fornece nenhuma evidência de falta de controle. Assim, o processo está sob controle.
Agora se o tamanho do subgrupo fosse o mesmo, teríamos que usar a carta NP. Vamos refazer o exemplo considerando o seguinte cenário:

Primeiro devemos calcular o Pbarra = 76/600 = 0,1266666667
Depois o NPbarra = 120*Pbarra = 15,2
Depois calculamos os limites de controle:
Limite superior = NPbarra – 3*sqrt[npbarra(1-pbarra)] = 15,2 – 3*sqrt[15,2(1-0,12667)] = 4,27
Limite superior = NPbarra + 3*sqrt[npbarra(1-pbarra)] = 15,2 + 3*sqrt[15,2(1-0,12667)] = 26,13
Por fim, plotamos os números de potes com defeito e os limites de controle:
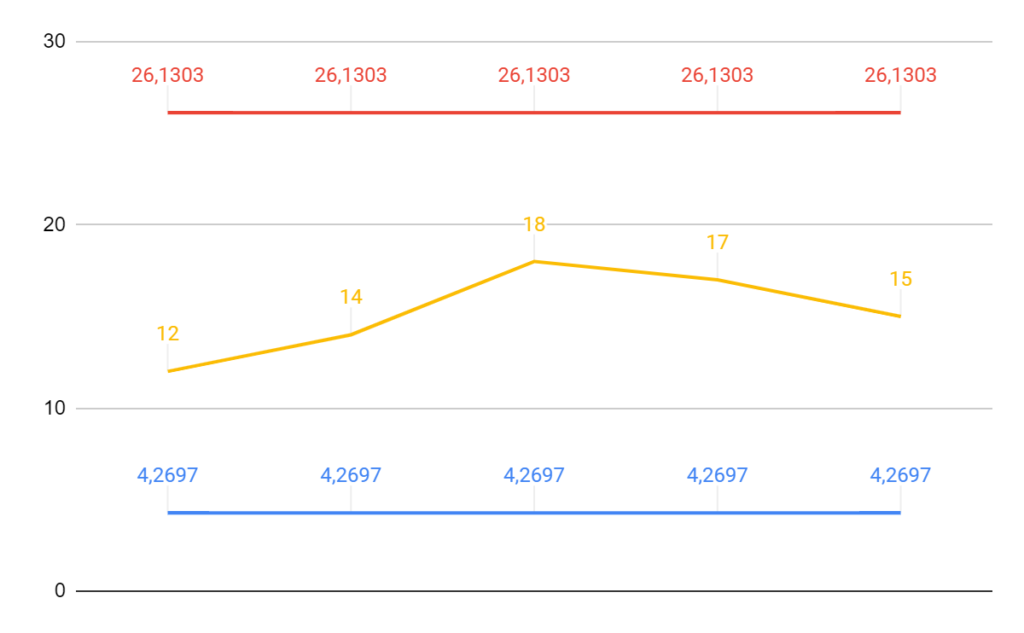
Neste caso a conclusão é semelhante a da carta P.
Uau! Quanta coisa nova não?! Que acham de deixarmos as cartas U e C para a próxima semana!?
Então, até la!