Dando sequência aos tipos de cartas de controle vamos falar hoje sobre a Carta IMR.
Estas cartas também devem ser aplicadas para dados contínuos, porém diferentemente da carta XBarra R, o subgrupo aqui deve ser de tamanho unitário.
Como assim tamanho unitário?
Imagine que está medindo algo que é extremamente caro, você pode ter várias “peças” disponíveis para medir? Pouco provável né! E se você estiver medindo algo que destrua sua peça? Concorda que só vai poder medir uma vez a peça, antes dela quebrar?!
Outras aplicações dessa carta ocorre quando temos dados coletados em hora temporal, por exemplo: a cada 1 hora coleto uma amostra.
Assim como a Xbarra R, temos 2 cartas aqui a I e a MR. A I é a carta individual e a MR é a carta de “Moving Range”.
A carta I tem a função de mostrar o comportamento dos dados ao longo do tempo e visa nos mostrar a presença ou não de possíveis problemas: “drifts” e “shifts”.
“Drifts” são sequências de valores crescendo ao longo do tempo ou descendo ao longo do tempo:
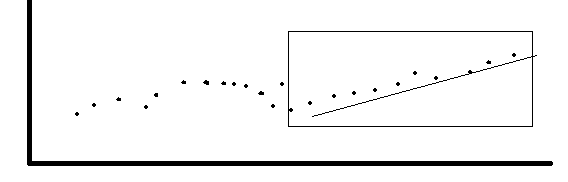
“Shifts” são mudanças bruscas de patamares:
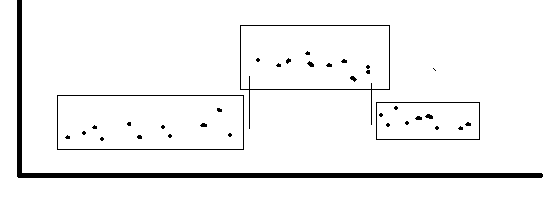
A carta MR é feita com os valores absolutos da diferença de cada valor pelo valor anterior. Ou seja ela mostra a variação de curto prazo e também possui um número a menos de dados que a carta I. Além disso também possui a função de avaliação de causa comum e especial.
Como a carta Xbarra R, a IMR também possuem limites que, neste caso são calculados da seguinte forma:
LSCMR = 3,267x(MRbarra)
Limite Superior Carta I =Média dos valores + 3x(MRbarra/1,128)
Limite Inferior Carta I =Média dos valores – 3x(MRbarra/1,128)
Vamos a um exemplo?
———————————————————————————————————————————–
Imagine que coletamos a altura de 10 pessoas e obtivemos os seguintes dados:
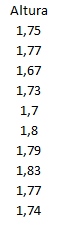
Vamos calcular os dados para fazer a carta MR da seguinte forma |1,77-1,75| =0,02, e assim sucessivamente, até termos 9 valores:
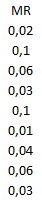
O Limite é calculado por 3,267(0,05) = 0,16335, onde 0,05 é a média dos valores MR.
Podemos assim plotar a carta:
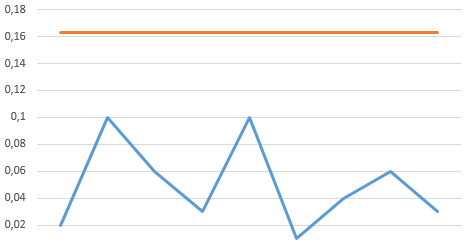
Podemos ver que não possuímos causas especiais e dando um indicativo da variação entre as medidas.
Para a carta I, precisamos calcular os limites de controle:
LSC = 1,755 + 3*(0,05/1,128) = 1,88
LIC = 1,755 – 3*(0,05/1,128) = 1,62
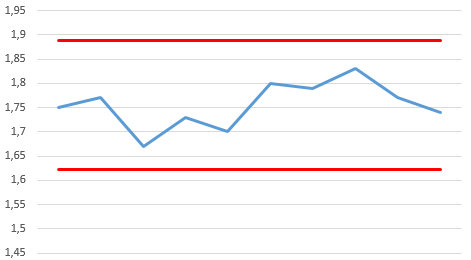
Nesta carta I, podemos ter um possível caso de shift, aparentemente tivemos uma mudança da média entre os 5 primeiros pontos e os 5 últimos. Vale a pena dar uma investigada a mais na coleta de dados, na sequência utilizada e até no sistema de medição!
Quanta coisas essas cartas nos contam não?
Até a próxima.